Beispiel 1

Subtraktion von 2-stelligen Zahlen. 

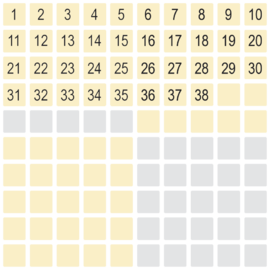
Beispiel 38 - 23 = 15

Der Beginn ist die Einstellung des Subtrahenden mit der Zahl 38.

Subtraktion von 2-stelligen Zahlen. 

Beispiel 38 - 23 = 15

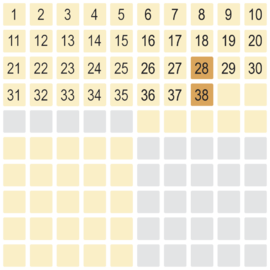
Der erste Schritt ist das Abziehen von zwei Zehner hier die 38 und die 28 in die Signalfarbenebene. 

Teilergebnis 38 - 20 = 18

Subtraktion von 2-stelligen Zahlen. 

Beispiel 38 - 23 = 15

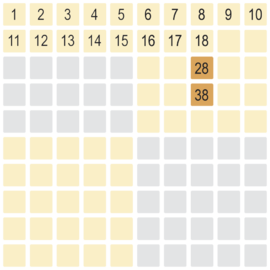
Der zweiter Schritt  bei der Rücksetzung auf die zwei Signalfarben  für die zwei  Zehner ist das Zurücksetzen der gelben Seiten von 37 - 29 und von 27 - 19 auf die Seiten ohne Zahlen, so dass die 18 als erstes Teilergebnis gut erkennbar ist.

 Teilergebnis 38 - 20 = 18

Subtraktion von 2-stelligen Zahlen. 

Beispiel 38 - 23 = 15

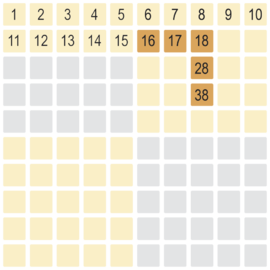
Der dritter Schritt  ist das Abziehen von den 3 Einer, hier die 18 - 16, 

auf die Signalfarben-Ebene. So ist das Endergebnis mit 15 gut erkennbar.

    38 - 20 - 3 = 15

    38 - 23 = 15

Beispiel 2

Subtraktion von 2-stelligen Zahlen mit Überschreitung des Zehnerbereriches 

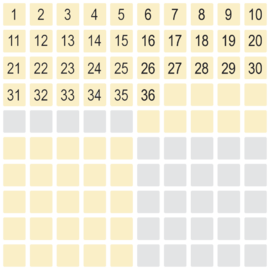
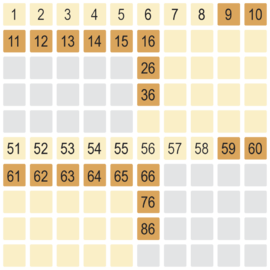
Beispiel 36 - 28

Der Beginn ist die Einstellung der Zahl 36 in gelben Farbton.

Subtraktion von 2-stelligen Zahlen. 

Beispiel 36 - 28

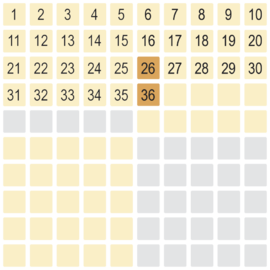
erster Schritt die Zehner kennzeichnen

Zuerst erfolgt auch hier der Abzug der 2 Zehner auf die Signalfarben-Ebene, hier die 36 und die 26. 

Teilergebnis 36 - 20 = 16

Subtraktion von 2-stelligen Zahlen. 

Beispiel 36 - 28

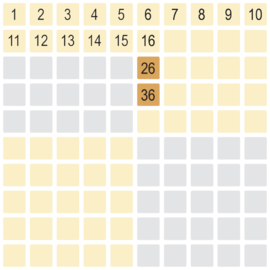
zweiter Schritt Rücksetzung der gelben Zahlen

Der zweite Schritt bei den den zwei Zehnersignalfarben ist die Rücksetzung von 35 - 27 und 25 -17 auf die Ebene ohne Zahlen.  Teilergebnis 36 -20 = 16

Subtraktion von 2-stelligen Zahlen. 

Beispiel 36 - 28 = 8

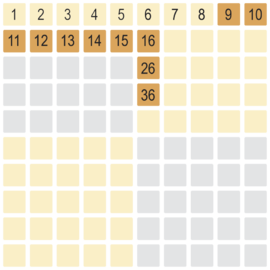
dritter Schritt Abziehen der acht Einer 36 - 20 - 8 = 8

Nun erfolgt der Einerabzug durch 8 Würfelumdrehungen ab dem Teil-ergebnis 16 von der 16 - 9 auf der Signalfarben-Ebene. So ist das Endergebnis, hier die 8, als erste gelbe Zahl vor den Signalfarbenzahlen

auch hier gut erkennbar.

           36 - 28 = 8

Subtraktion von 2-stelligen Zahlen. 

Beispiel 36 - 28 = 8

Mit einem weiteren Beispiel für   86 - 28 = 58